Vi har tidigare i kursen bestämt geometriska sannolikheter med hjälp av programmering. Samma metod kan användas för att uppskatta areor och därmed integraler.
Låt \(s(x)\) vara funktionen du definierade i uppgift 6. Antag att \(y=s(x)\) på intervallet \(0\le x\le1\) uppfyller \(s(x)<A\). Då kan vi definiera en rektangel \(0\le x\le1\), \(0\le y\le A\). Denna rektangel har area \(A\). En del av denna rektangel utgörs av arean mellan \(y=s(x)\) och \(x\)-axeln, alltså området vars area är \(I=\int_0^1s(x)dx\).
Genom att slumpa punkter \((x,y)\) i rektangeln och bestämma andelen slumpade punkter med \(y<s(x)\) kan integralen \(I\) uppskattas eftersom denna andel borde närma sig \(I/A\).
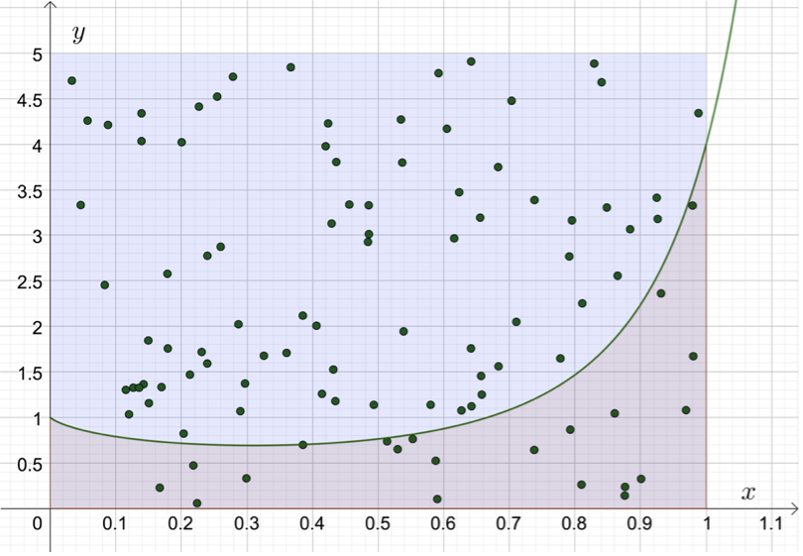
I figuren nedan väljs \(A=5\) och 100 punkter \((x,y)\) har slumpats i rektangeln.

Av dessa uppfyller 21 st \(y<s(x)\) så att \[int_0^1s(x)dx\approx0,21\cdot5=1,05\] vilket är ca 9 % mindre än det verkliga värdet av integralen.
Implementera denna metod för att beräkna integralen du beräknade i föregående uppgift med trapetsregeln. Ungefär hur många punkter behövs för att få samma noggrannhet? Vilken metod verkar vara mest effektiv i detta fall?
Om du vill ha hjälp så finns pseudokod i länken nedan.