
Arean mellan kurvan \(y=f(x)\) och \(x\)-axeln mellan \(x=a\) och \(x=b\) ges som bekant av integralen \(\int_a^bf(x)dx\) så länge kurvan ligger över \(x\)-axeln. Om funktionsuttrycket är känt kan vi ofta beräkna integralens exakta värde med hjälp av integralkalkylens fundamentalsats \[\int_a^bf(x)dx=F(b)-F(a).\] Detta kräver dock att vi kan bestämma den primitiva funktionen \(F\). De matematiska tekniker ni lärt er till och med Ma3c är tyvärr inte tillräckliga för att bestämma primitiva funktioner till alla funktioner av intresse. Även om ni hade läst Matematik 99c skulle vissa primitiva funktioner vara ”omöjliga” att bestämma. Vi vill nämligen gärna att den primitiva funktionen ska vara elementär, vilket innebär att den kan konstrueras genom en ändlig kombination av de funktionstyper vi stött på hittills: potensfunktioner, exponentialfunktioner, logaritmer och trigonometriska funktioner. Joseph Liouville visade dock 1835 att det existerar elementära funktioner som inte har någon elementär primitiv funktion. Det krävs alltså andra metoder för att beräkna integralers värde.

Joseph Liouville (1809-1882)
Ett sätt att beräkna ett närmevärde till en integral är genom att använda Riemannsummor där motsvarande area uppskattas med rektanglar. En mer effektiv metod kallas trapetsregeln och bygger på att uppskatta arean med hjälp av parallelltrapetser. I figuren nedan illustreras metoden för \(f(x)=x^3-5x^2+10x-2\) i intervallet \(1≤x≤3\). Det man gör är att ersätta funktionen med räta linjestycken i ett antal delintervall. Med fler delintervall fås en bättre uppskattning av integralens värde.
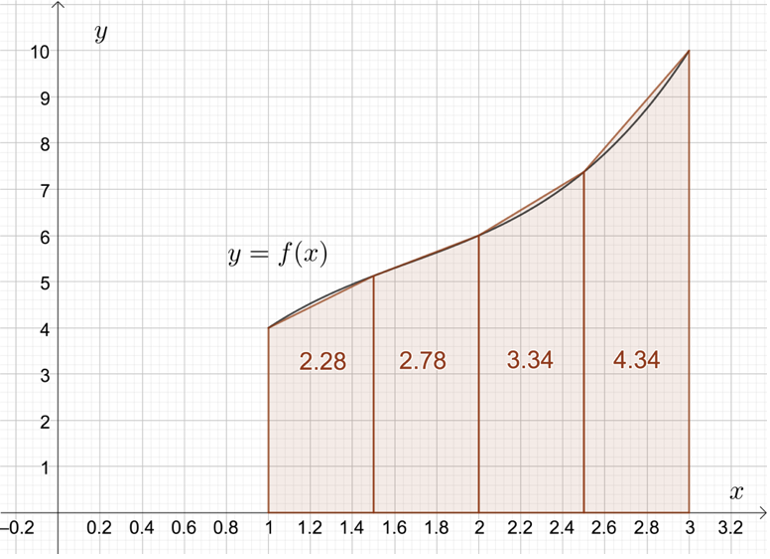
Arean av ett parallelltrapets är \[A=h(a+b)/2\] där \(h\) betecknar höjden (horisontell i figuren ovan) och \(a\) och \(b\) de två parallella sidorna.
Intervallet delas in i fyra lika stora intervall och vi får därför höjden \(h=(3-1)/4=0,5.\) Arean av parallelltrapetserna är \[\scriptstyle \begin{eqnarray}A&=&A_1+A_2+A_3+A_4\\ &=&(0,5⋅(f(1)+f(1,5)))/2+(0,5⋅(f(1,5)+f(2)))/2+(0,5⋅(f(2)+f(2,5)))/2+(0,5⋅(f(2,5)+f(3)))/2\\ &=&0,5/2 (f(1)+2f(1,5)+2f(2)+2f(2,5)+f(3))\\ &\approx&12,74\end{eqnarray}\] Notera att första och sista funktionsvärdet endast förekommer en gång medan de mellanliggande alla förekommer två gånger. Förstår du varför det är så?
Integralen kan beräknas exakt och värdet är \(38/3\approx12,67\). Felet i vår approximation är alltså 0,55 %. Felet är litet eftersom vår funktion inte ändras så snabbt i intervallet. Ju snabbare funktionen ändras, desto fler delintervall behövs.
I allmänhet så kan trapetsregeln med N delintervall beskrivs med formeln nedan \[\int_a^bf(x)dx\approx \frac{h}{2}(f(a)+2f(a+h)+f2(a+2h)+⋯+2f(a+(N-1)h)+f(b))\] där \(h=(b-a)/N\). Denna formel vill vi implementera i Python.