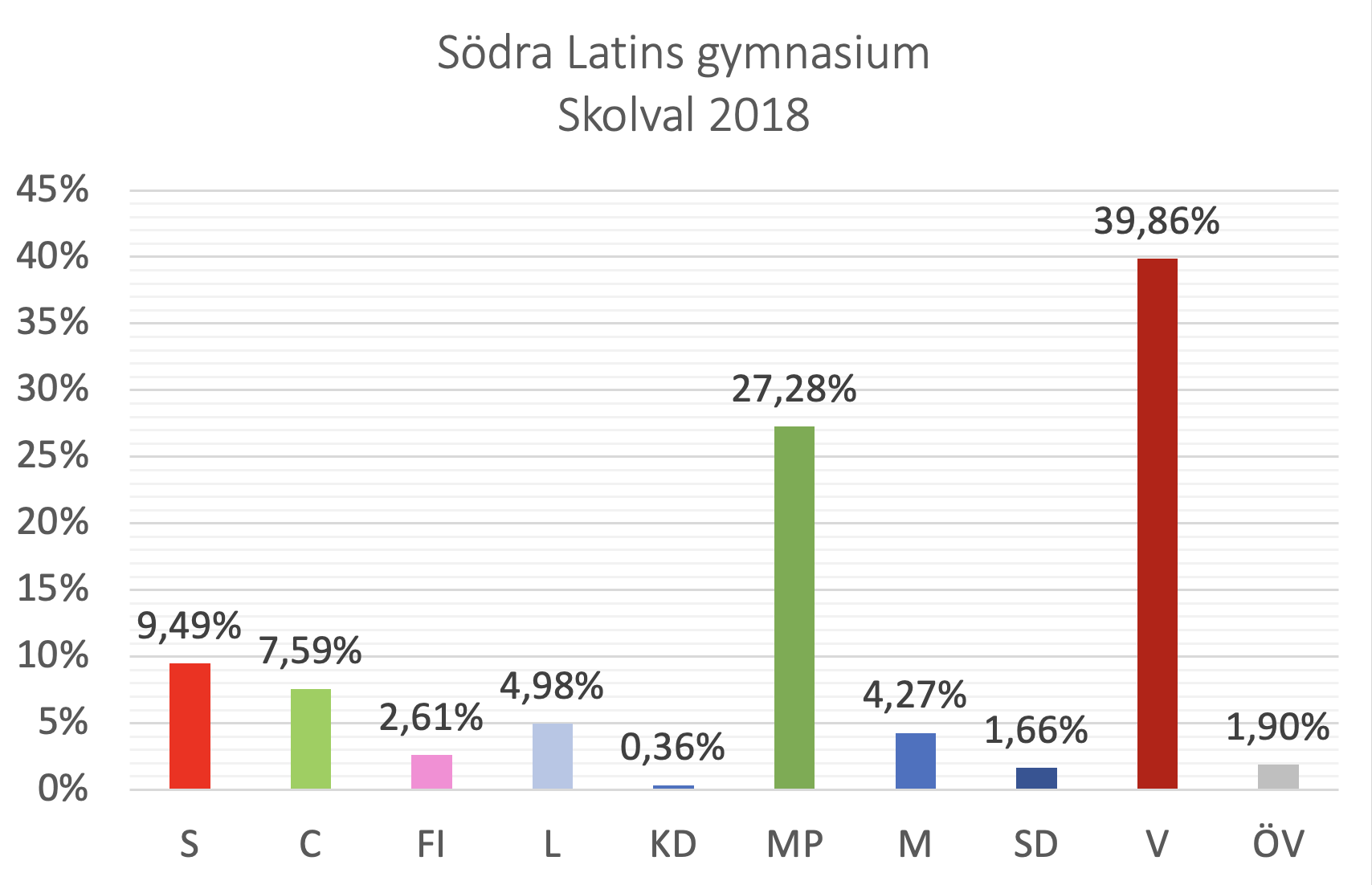
Vid skolvalet på Södra Latin 2018 fördelades rösterna enligt diagrammet nedan. Antalet giltiga röster var 843.

Vi är intresserade av skillnaden mellan röstandelen i ett stickprov och den verkliga röstandelen. Vi kallar absolutbeloppet av denna skillnad för avvikelsen . För att göra detta används ett program som simulerar valresultatet i en population som röstar precis som eleverna vid Södra. Alltså, om populationen är 1000, så kommer 43 personer rösta på Moderaterna.
from random import *
population = []
antal = 843
stickprov = []
n = 64
partier = ('M', 'C', 'L', 'KD', 'S', 'V', 'MP', 'SD', 'FI', 'ÖV')
röstandel = (0.0427, 0.0759, 0.0498, 0.0036, 0.0949, 0.3986, 0.2728, 0.0166, 0.0261, 0.0190)
for i in range(0, len(röstandel)):
for j in range(0,int(röstandel[i]*antal)):
population.append(partier[i])
for i in range(0, n):
index = randint(0, len(population) - 1)
tmp = population.pop(index)
stickprov.append(tmp)
print('Parti\t', 'Verkligt (%)\t', 'Stickprov (%)\t', 'Skillnad (procentenheter)')
for i in range(0, len(partier)):
andel = 100*stickprov.count(partier[i])/n
print(partier[i],'\t\t', round(100*röstandel[i],2), '\t\t\t', round(andel, 2),'\t\t\t', abs(round(100*röstandel[i]-andel,2)))
Ändra i koden ovan så att populationen är lika med antalet giltiga röster i skolvalet och urvalet är två klasser, 64 elever. Kör programmet och se att det fungerar.
Fråga 1
De första nästlade for-looparna går igenom alla partier och skapar en lista med röster. Det kommer att finnas lika många ”M” i listan som antal röster på M.
Hur många ”M” finns det i listan?
Fråga 2
Den andra for-loopen (inte den nästlade) slumpar fram ett index och plockar ut motsvarande röst ur listan med röster. Detta upprepas n gånger, där n är stickprovets storlek.
Hur många element kommer finnas i listan ”stickprov”?
Fråga 3
Den sista for-loopen skapar en tabell med fyra kolumner; parti, verklig röstandel, röstandel i stickprovet och skillnaden mellan verklig röstandel och röstandel i stickprovet.
För vilka partier blev avvikelsen störst respektive minst?
Om du kör programmet flera gånger kommer röstandelen i stickprovet givetvis att variera. Alltså kommer avvikelsen att variera. Vi är intresserade av att uppskatta avvikelsens genomsnittliga storlek för olika storlekar på population och stickprov.
Fråga 4
Bestäm medelvärdet av avvikelsen för det största respektive minsta partiet. Använd minst 10 körningar.
Fråga 5
I Sverige röstade 6 535 271 personer i senaste riksdagsvalet (2018). Antag att dessa personer röstade precis som eleverna på Södra Latin. Behåll stickprovets storlek (64), men ändra i koden så att populationen motsvarar antalet röstande i riksdagsvalet 2018.
Bestäm medelvärdet för avvikelsen för det största respektive minsta partiet. Använd minst 10 körningar.
Fråga 6
Ändra stickprovets storlek till 1 000.
Bestäm medelvärdet för avvikelsen för det största respektive minsta parti. Använd minst 10 körningar.
Fråga 7
Hur stor andel av populationen utgjorde stickprovet i uppgift 4 respektive 6? När blev avvikelsen minst?
Fråga 8
Jämför resultaten i uppgift 4, 5 och 6. Vilket av dessa tre alternativ bör ge minst avvikelse?
Testa också med hjälp av programmet.